Pizza Problem Posed to me by an Egyptian guy

gregoriousmaths25th Mar 2022Uncategorized

(Shoutout to camelman for the problem)

The problem:

Given a pizza, what is the most amount of slices one can obtain by cutting it with straight lines $n$ times?

Some experimentation:

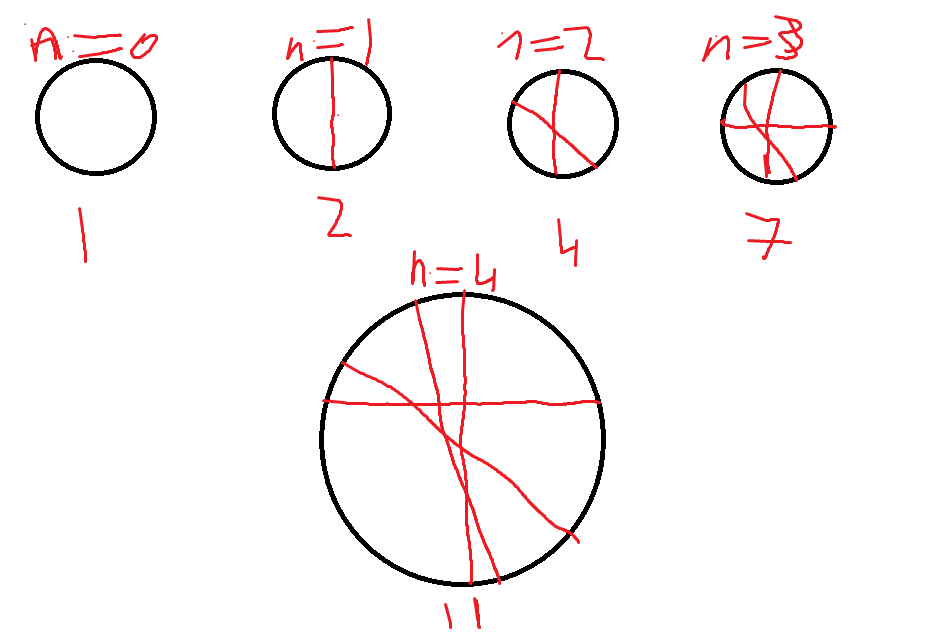
The first 5 pizzas, having been cut $n$ times.

The first 5 pizzas, having been cut $n$ times.

The way to generate the most slices:

The trick for getting as many slices as possible every time is to draw a line that intersects every other line that has been drawn. That is, if there have been $n$ slices, the $(n+1)$ th slice must intersect all of those lines. The problem now is to express this as a formula of the form

$\text{number of slices after }n\text{ cuts}=f(n)$ .

Expressing it as $f(n)$ :

Note that if the $(n+1)$ th line crosses $n$ lines then it has cut through $n+1$ old slices. Therefore, given $f(0)=1$ , we have:

$f(1)=f(0)+(0+1)=1+1=2$

$f(2)=f(1)+(1+1)=2+2=4$

$f(3)=f(2)+(2+1)=4+3=7$

$f(n+1)=f(n)+(n+1), \, f(0)=0$

These are precisely the triangular numbers plus 1, and the formula for the $n$ th triangular number is

$\frac{n^2+n}{2}$

so our desired formula is

$\boxed{f(n)=\frac{n^2+n}{2}+1=\frac{n^2+n+2}{2}}$

Published by gregoriousmaths

I am an aspiring mathematician and am using this blog to post my mathematical notes on random topics in maths- hopefully you find them helpful! View more posts

Leave a comment Cancel reply