Some Half Baked Thoughts on Spectral sequences

Spectral sequences are among one of the most useful tools for topology, geometry and algebra. However, they have the reputation for being difficult to grasp.

Roughly, they approximate the homology $H^{\ast}$ of some chain complex, by breaking it up into many little pieces. A nice example of this arises in topology, where we can filter such a complex:

$\textbf{Motivation:}$

Recall that, given a space $X$ , we may form the cohomology ring

$H^{\ast}(X)=\bigoplus_{n}H^n(X)$

which is graded, by the cup product:

$\smile: H^{m}(X)\times H^{n}(X)\to H^{n+m}(X)$

which, up to degrees, is commutative:

$x\smile y=(-1)^{|x||y|}y\smile x$ .

Our goal is to compute this cohomology ring. For simplicity, let $X$ be a CW cell complex and $A\hookrightarrow X$ be a CW pair. Then this induces a long exact sequence in cohomology:

$\dots\leftarrow H^{n}(X)\leftarrow H^{n}(A)\leftarrow H^{n}(X,A)\overset{\delta}{\leftarrow} H^{n-1}(X)\leftarrow\dots$ .

This is good; we can use this to help us with our computations- but why stop here? We now introduce a filtration to the mix:

$A_0\hookrightarrow A_1\hookrightarrow X$

which, similarly, induces two long exact sequences in cohomology. Hopefully, one can see where we are going: introducing a filtration of the form

$A_{0}\hookrightarrow A_{1}\hookrightarrow\dots\hookrightarrow A_{n}=X$

will give us many long exact sequences in cohomology which will help to approximate the cohomology of $X$ . The method for storing all of this data is called a spectral sequence.

$\textbf{Formal Definitions:}$

$\textit{Definition:}$ We say that a collection $\{E^{p,q}_{r}, d_{r}\}$ is a spectral sequence if:

For all $p,q,r>0,\, E_{r}^{p,q}$ is an abelian group.
The differentials $d_{r}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1}$ satisfy $d^{2}=0$
The homology of the $r$ th page is the $r+1$ th page. That is: $H(E^{p,q}_{r}; d{r})=E_{r+1}^{p,q}$

The $E_1$ page- each differential goes across the $p$ axis by one and doesn’t move up or down the $q$ axis.

The $E_1$ page- each differential goes across the $p$ axis by one and doesn’t move up or down the $q$ axis.

The $E_{2}$ page- the differential goes across by 2 in the $p$ axis and now down by 1 in the $q$ axis.

The $E_{2}$ page- the differential goes across by 2 in the $p$ axis and now down by 1 in the $q$ axis.

$\textit{Definition:}$

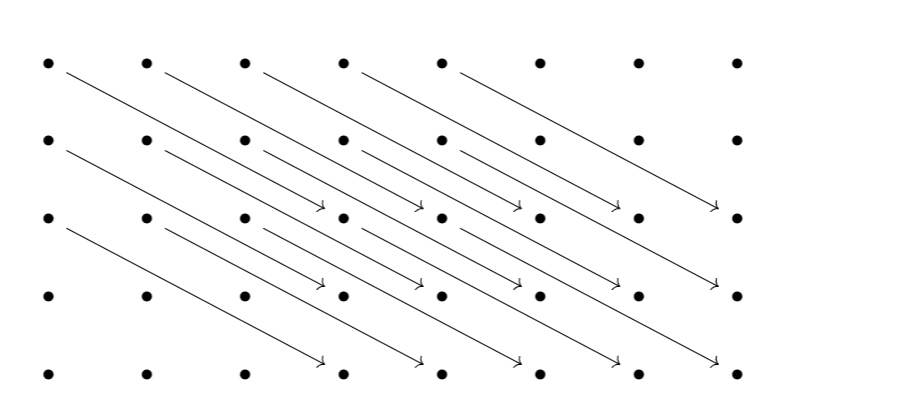
We say that the spectral sequence collapses at the $r$ th page if:

$E_{r}=E_{r+1}=\dots=E_{\infty}$ .

Furthermore, we say that the spectral sequence converges to a graded object $H^{\ast}$ if we can sum along the diagonals to get:

$H^n=\bigoplus_{p+q=n}E^{p,q}_{\infty}$ , modulo certain extension problems.

When this happens, we write $E_{2}^{p,q}\implies H^{\ast}$ .

$\textbf{Constructing Spectral Sequences:}$

I shall finish this blog post by talking about exact couples how to construct the Bockstein spectral sequence, using exact couples, as an example.

$\textit{Definition:}$

We say that $(D,E,i,j,k)$ is an exact couple (where $E$ and $D$ are modules) if the following diagram is exact at each vertex:

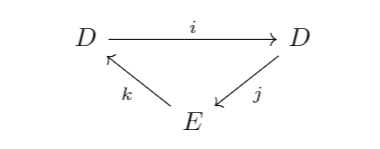
But now things get interesting. We can set $d:E\to E$ as being $d=jk$ . Note that $d$ satisfies $d^2=0$ since:

$d^2=(jk)(jk)=j(kj)k=0$

by the exactness of the diagram. So it makes sense to introduce the notion of the derived couple.

$\textit{Definition:}$

Given an exact couple $(D,E,i,j,k)$ , we define the derived couple $(D',E',i',j',k')$ as follows:

$D'=i(D)$
$E'=H_{\ast}(E; d)$
$i'=i\vert_{i(D)}$
$j'(i(x))=j(x)+jk(E)=[j(x)]$
$k'([y])=k(y)$

$\textit{Proposition:}$

The derived couple is exact.

Therefore, we can iterate this process to get infinitely many exact couples $(D^r, E^r, i^r, j^r, k^r)$ :

$(D^1, E^1, i^1, j^1, k^1)=(D,E,i,j,k)$
$(D^2, E^2, i^2, j^2, k^2)=(D', E', i', j', k')$
$(D^3, E^3, i^3, j^3, k^3)= (D'', E'', i'', j'', k'')$
$\dots$

If we let $d^r=j^rk^r$ , then $(E^r, d^r)$ is an example of a spectral sequence. We now move onto the Bockstein spectral sequence construction:

$\textbf{Constructing the Bockstein Spectral Sequence:}$

Recall that we have a short exact sequence of groups:

$0\to\mathbb{Z}/p\mathbb{Z}\to\mathbb{Z}/p^2\mathbb{Z}\to\mathbb{Z}/p\mathbb{Z}$

which yields a short exact sequence of chain complexes:

$C\otimes\mathbb{Z}/p\mathbb{Z}\to C\otimes\mathbb{Z}/p^2\mathbb{Z}\to C\otimes\mathbb{Z}/p\mathbb{Z}\to 0$

and hence a long exact sequence in homology whose boundary map $\beta: H_{n}(C;\mathbb{Z}/p\mathbb{Z})\to H_{n-1}(C;\mathbb{Z}/p\mathbb{Z})$ is called the mod $p$ Bockstein.

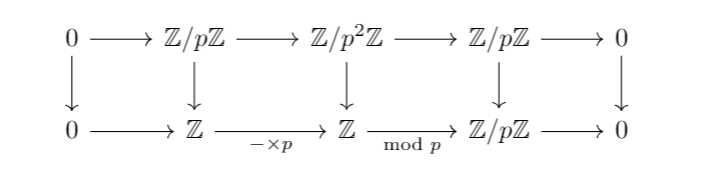
The following commutative diagram of short exact sequences shows that $\beta$ factors as a composition

$\beta: H_{n}(C;\mathbb{Z}/p\mathbb{Z})\overset{\partial}{\to} H_{n-1}(C; \mathbb{Z})\to H_{n-1}(C; \mathbb{Z}/p\mathbb{Z}$ .

Therefore, we have an exact couple

where the maps are induced by the short exact sequence $0 \to \mathbb{Z} \to \mathbb{Z} \to \mathbb{Z}/p\mathbb{Z}\to 0$ . The differential $d^1$ is given by $\beta$ and $d^r=\beta^{(r)}$ is called the $r$ th Bockstein homomorphism. It turns out that: