Warm up for the talk: Categories

Because of my upcoming video about higher category theory, I thought I would make this short blog post introducing categories and some related ideas about them. Therefore, this will be a pretty long blog post, with lots of advanced examples sprinkled in (they aren’t necessary for actually understanding the category theory itself, but they are really cool examples of how we can translate concepts from different areas of maths into category theory).

Introduction:

In category theory, there are certain concepts that pop up all the time. One of the most common is the “universal property”. This is a certain defining property which describes an object in a certain category

Example 1

Given a set $X$ and an element $x\in X$ , there is a unique map

$X\to\{x\}$

which is given by mapping any element $X\ni x'\mapsto x$ . This means that, given a set $X$ , an element $\{x\}\in X$ has the universal property that there is a unique map

$X\mapsto \{x\}$

Example 2

In topology, the discrete topology on a set $S$ has the unique property that any map

$DS\to X$

is continuous. More precisely, let $S$ be the underlying set, $DS$ be the set equipped with the discrete topology, and $X$ be any topological space. Then, given the functions:

$i:S\to DS\, ,s\mapsto s$

$f:X\to S$

where $f$ is arbitrary, then there is a unique continuous map

$\bar{f}:DS\to X$

such that

commutes. Let’s unpack this a little bit more: the commutativity of the diagram means that $\bar{f}\circ i(s)=f(s)$ for all $s\in S$ . More precisely, since $i(s)=s$ , this means that $\bar{f}(s)=f(s)$ . This is true for all topologies, you may scream, however in that case you are forgetting the requirement that $\bar{f}$ is continuous. Therefore, all this is saying is that any function $f:S\to X$ can be made continuous if you let $S$ have the discrete topology. This is a universal property since this is only true for the discrete topology. Consider, for example, trying to replace $DS$ with the indiscrete topology. The statement would fail horribly in that case! However, the indiscrete topology does give rise to a similar universal property. It is, what is known as the dual of the discrete topology. Essentially, what this means about the universal property is that all of the arrows in the diagram above will be reversed. That is, the diagram will now look like:

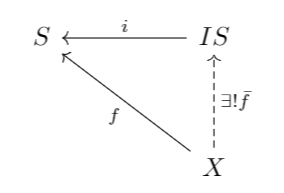
with the same explanation as before, except that this time the indiscrete topology has the universal property that any map

$X\to IS$

is continuous rather than any map

$DS\to X$

being continuous which was the universal property of the discrete topology.

Categories:

Definition 1

A (small) category $\mathscr{C}$ is a collection of objects along with the following data:

A set $\mathrm{Ob}(\mathcal{C}$ of objects
A set $\mathrm{Hom}_{\mathcal{C}}(A,B)$ of arrows (or morphisms) between two objects $A$ and $B$ .
For a triple $A, B, C$ of objects, there is a composition law

$\circ:\mathrm{Hom}_{\mathcal{C}}(A,B)\times\mathrm{Hom}_{\mathcal{C}}(B,C)\to\mathrm{Hom}_{\mathcal{C}}(A,C)$

which we denote $f\circ g\in \mathrm{Hom}_{\mathcal{C}}(A,C)$

We may also write compositions as follows:

$A\overset{f}{\to} B\overset{g}{\to} C$

The composition law must be associative and unital, that is: for any $f\in\mathrm{Hom}_{\mathcal{C}}(A,B)\, ,g\in\mathrm{Hom}_{\mathcal{C}}(B,C)$ and $h\in\mathrm{Hom}_{\mathcal{C}}(A,C)$ we have it that:

$f\circ (g\circ h)=(f\circ g)\circ h$

and there is a morphism $\mathrm{id}$ called the identity such that

$f\circ\mathrm{id}=f$ and $\mathrm{id}\circ f=f$ .

Example 1

Consider the category Top of topological spaces, where the morphisms would be continuous maps.

Example 2

Consider the category Ab of abelian groups, or Grp of groups, where in both cases the morphisms are group homomorphisms.

Example 3

Consider the category Set of sets, where the morphisms are just functions.

Functors:

Definition 2

A (covariant) functor $F:\mathscr{C}\to\mathscr{D}$ is a map of categories. It assigns an object $A\in\mathscr{C}$ to an object $F(A)\in\mathscr{D}$ . Furthermore, it will assign a to morphism $f$ between objects in $\mathscr{C}$ to another morphism $F(f)$ in $\mathscr{D}$ such that:

$F(\mathrm{id}_A)=\mathrm{id}_{F(A)}$ and $F(g\circ f)=F(g)\circ F(f)$

or if $F(g\circ f)=F(f)\circ F(g)$ then $F$ is called a contravariant functor.

Definition 3

Given a category $\mathscr{C}$ , we say that $\mathscr{C}^{op}$ is the opposite category of $\mathscr{C}$ if:

$\mathrm{Ob}(\mathscr{C})=\mathrm{Ob}(\mathscr{C}^{op})$
$\mathrm{Hom}_{\mathscr{C}}(A,B)=\mathrm{Hom}_{\mathscr{C}^{op}}(B,A)$

There are of course many very interesting examples of functors:

Example 1

We have so called “forgetful functors” which drop the added structure of the underlying set. For example:

$F:\textbf{Grp}\to\textbf{Set}$

which just sends a group $(G,+)$ to the underlying set $G$ and so on (there are many examples of such functors).

Example 2

The fundamental group $\pi_1$ is a functor

$\textbf{Top}_*\to\textbf{Grp}$

Example 3

The delooping of a group is a functor too. What the delooping of a group does is describe a group as a groupoid with one object. More precisely, given a group $G$ , the delooping of $G$ , denoted $BG$ is a groupoid (category where all morphisms have an inverse) with one object $g$ and morphisms

$(\mathrm{Hom}_{BG}(g,g),\circ)=G$

elements of $G$ , composition is multiplication in $G$ , identity morphism is the identity element in $G$ and the inverse morphisms are inverse elements in $G$ . So $B$ is a functor

$B:\textbf{Grp}\to\textbf{Grpd}$

Example 4

The fundamental groupoid of a space $X$ is a groupoid which assigns to a topological space $X$ a groupoid $\Pi(X)$ which has:

$\mathrm{Ob}(\Pi(X))=$ points in $X$
$\mathrm{Hom}_{\Pi(X)}(x,y)=\{\text{Set of paths } x\to y\}/\simeq$

But how exactly does it extend to a functor? The answer is that it extends to a groupoid

$\Pi:\textbf{Top}\to\textbf{Grpd}$

by sending a space $X$ to a groupoid $\Pi(X)$ and a map

$f:X\to Y$ to a morphism $f_*:\Pi(X)\to\Pi(Y)$ which sends $f_*([\alpha])=[\alpha\circ f]$ .

Natural Transformations:

A natural transformation can be thought of as a morphism between functors.

Definition 1:

A natural transformation $\xi:F\to G$ between functors consists of a morphisms $\xi_A:F(A)\to G(A)$ such that:

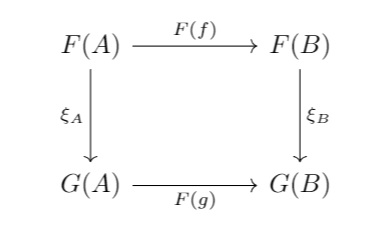
commutes.

Definition 2

We say that $\xi$ is a natural isomorphism if every single $\xi_A$ is an isomorphism for every object $A\in\mathscr{C}$ . Two functors are isomorphic if there is a natural isomorphism $F\to G$ .

Example 1

A statement like

“A group is isomorphic to its opposite group”

can be expressed in terms of a natural isomorphism. More precisely, define the opposite of a group $(G,+)$ , $(G^{op},+^{op})$ to be the same set as $G$ but the operation is given by $a+^{op}b=b+a$ .

We can quickly move down to functors by defining

$Op(f):\textbf{Grp}\to\textbf{Grp}$ , $Op(f)=f$

It is in fact a group homomorphism since

$Op(f)(a+^{op}b)=f(a+^{op}b)=f(b+a)=f(b)+f(a)=f(a)+^{op}f(b)=Op(f)(a)+^{op}Ob(f)(b)$

Now we can move up a level to natural transformations by saying:

The identity functor $\textbf{Id}:\textbf{Grp}\to\textbf{Grp}$ is naturally isomorphic to the functor $Op:\textbf{Grp}\to\textbf{Grp}$

And so we have rephrased “A group is isomorphic to its opposite group” in terms of natural transformations.

Example 2

In algebraic topology, the Hurewicz homomorphism is also a natural transformation! This is because both

$\pi_n:\textbf{Top}_*\to\textbf{Grp}$

and

$H_n:\textbf{Top}_*\to\textbf{Grp}$

are functors, the Hurewicz homomorphism is natural for all $n\geq 0$ and the following diagram commutes:

A Glimpse at Higher Category Theory: The 2-Category of Categories

In order to avoid paradoxes and size issues like Russel’s paradox when talking about the “category of categories”, we restrict ourselves to small categories.

Now we have a tiny glimpse at higher category theory. In the category of small categories, we have the following data:

Objects are just small categories
Morphisms are functors
2-morphisms are natural transformations

But what are $2$ -morphisms? Well, they are what they sound like: morphisms between morphisms. One of the ideas behind higher category theory is to study such “higher morphisms”. It is hard to make precise the case when we have higher morphisms between morphisms, higher morphisms between those ones and so on forever. However, that is for the talk to make precise….

Warm up for the talk: Categories

Published by gregoriousmaths

Leave a comment Cancel reply

Share this:

Related

Published by gregoriousmaths

Leave a comment Cancel reply